Measuring the Wavelength of Microwaves

For our WISE project, we studied and measured the wavelengths of microwave radiation. These particular radio waves are of short wavelength, and travel at the speed of light. Radio waves and light are both types of electromagnetic radiation and travel at the same speed. The picture below displays a transmitter (shown on the left) and receiver (shown on the right). The transmitter produces microwaves that are picked up and read by the receiver. Click on any of the pictures to get a larger view.

We measured the distance between the emitter and the receiver and then recorded the relative intensity of the microwaves at that distance. In the process of doing this, the microwaves set up a standing wave, much like the one created when two people at opposite ends grab hold of a slinky and shake it (picture). Standing waves have points of maximum constructive interference and points of maximum destructive interference that alternate with each other. As you can see, this is evident because the graph that we made shows the fluctuating intensity that looks like a roller coaster going down, up, down, up, etc.

We made our graph showing the relationship between the relative intensity of the microwaves and the distance between the microwave emitter and the receiver using Microsoft Excel. By analyzing the interference pattern we found a value for the wavelength of the microwave radiation of 2.85 cm. We obtained this value by calculating the change in the receiver's distance from one peak to another, divided by the number of complete cycles in between.

On one of our WISE sessions we met with a Kevin, a graduate student, to measure the frequency of the microwave transmitter. Unfortunately, we were not able to ascertain an exact number, due to unexpected frequency shifts. The frequency shifted approximately by one to two percent at a rapid rate, making it impossible to obtain a reading. If we had found the frequency of the electromagnetic wave, we would have been able to calculate the size of the wavelength by using the equation depicted below.

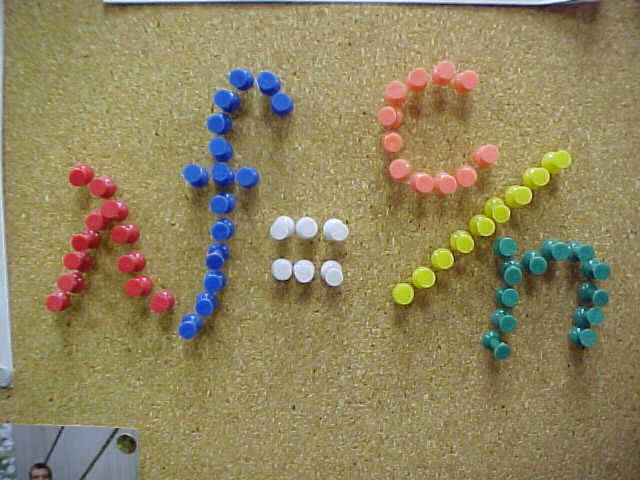
The first letter of the equation (red colored pins) is the Greek letter lambda. Lambda is the symbol used to represent wavelength. The next letter is f. Lower case f is used to represent the frequency. The letter "c", which is the same letter c that is used in Einstein's famous equation E=mc², represents the constant value for the speed of light in a vacuum. That value is exactly 29,979,245,800 centimeters per second. The letter n represents the absolute index of refraction of the medium which the electromagnetic wave is passing through, which in our case is air. The index of refraction of air is very close to 1.00. By dividing the speed of light c by the wavelength value that we found (lambda = 2.9 cm) we were able to determine the frequency, which is f = 10.3 Ghz. This frequency is about four times higher than that used in a standard home microwave oven.