Demonstrating Total Internal Reflection

Introduction

The idea for this project evolved after various discussions about Total Internal Reflection (TIR).Total Internal Reflection is a phenomenon that can occur when a ray of light passes from one medium to another with a lower index of refraction. If the angle of incidenc at the boundary is larger than the "critical angle" then the ray will be perfectly reflected with no loss of energy. The critical angle can be determined using Snell's Law. The critical angle is equivalent to the angle of incidence at which the angle of refraction is 90 degrees.

Inspired by a paper by D.C. Look Jr, I decided to duplicate the experiment he conducted. The paper titled "Novel Demonstration of Total Internal Reflection" provides an alternative method of measuring the index of refraction of an unkown liquid. In order to carry out this experiment, I used a green laser beam, a liquid placed in a container, and a white diffusely reflecting undersurface.

Deriving the Formula

When we first came across this paper, we started to think of ways in which we could make this a simple experiment in order to determine the index of refraction of a liquid. We decided to use water as our liquid and then conduct the experiment to test out the validity of the equation given. According to the paper, if we set up everything correctly, the index of refraction could be measured using the formula:

In order to get a better understanding of the experiment, we decided to derive the formula using our knowledge of optics and came to the conclusion that the formula is related to the geometry. Here is a diagram of what is happening inside the water tank.

When a laser is directed normal to the surface of the water, it hits the container at point A. Due to the white sheet of paper placed directly under the water, the light ray undergoes a diffused reflection. Some of the reflected rays refract back into the air. However, when the angle is large enough (critical angle), the light rays undergo Total Internal Reflection and the rays hit the container at point B. This is when you observe a dark circle with light around it. The distance from point A to point B is the radius of the circle.

Using Snell's Law, we figured out that the sine of the critical angle was equal to (1/n) where n is the index of refraction of water. With keeping this fact in mind and using trigonometry, we derived the formula that was given in the paper.

Ideas

Our first instinct in this experiment was to get a container and place the white piece of paper under the container. When we filled up the container with water and directed the laser normal to the surface, we saw that instead of a dark circle with light around it, we observed a light circle with darkness around it. After thinking about it a little, we decided to put the white sheet of paper directly under the water. This was when we observed what we were supposed to see.

One of the most important steps in this experiment was measuring the radius. In order to be as accurate as possible, Dr. Noe suggested that I create a circular ruler using a program called xfig. Here is a picture of the ruler:

Another thing we had to figure out was how we were going to measure the depth of the water. We had to figure out how we were going to get around the meniscus to get an accurate measurement of the depth. Later, we realized that the easiest way would be read the measurement from under water since our container was translucent.

Problems

One of the biggest problems we faced was the floating of the white sheet of paper. We tried several different ways to keep the paper from floating up. We used weights to hold it down, we tried taping the paper to the bottom, and then we tried placing the paper on a heavier weight and then placing it under water. However,as the water level increased, the paper always floated up. This made the radius appear smaller than it was and therefore gave us results that did not make sense.

Another problem we faced during this experiment was making sure that the bottom of the container was parallel to the upper surface of the water. We used a level to check this and realized that the original container that we were using was not good enough. Therefore, we had to switch to another container to make sure that the bottom of this container would not make the radius of the circle look larger or smaller than it was.

We finally decided to glue the paper to the bottom of the container to ensure that it would not move once we started adding water.

Final Trial

After I glued the circular ruler to the bottom of the container, we decided that we were going to measure the depth of water for several radii and then plot it on a graph to get better results.

Here is the data I collected and then analyzed with Excel. The line is the best linear fit through the points.

Radius (cm)	2.0	3.0	4.0	5.0	6.0	7.0	8.0	9.0
Height (cm)	0.9	1.4	1.75	2.25	2.7	3.25	3.6	4.2

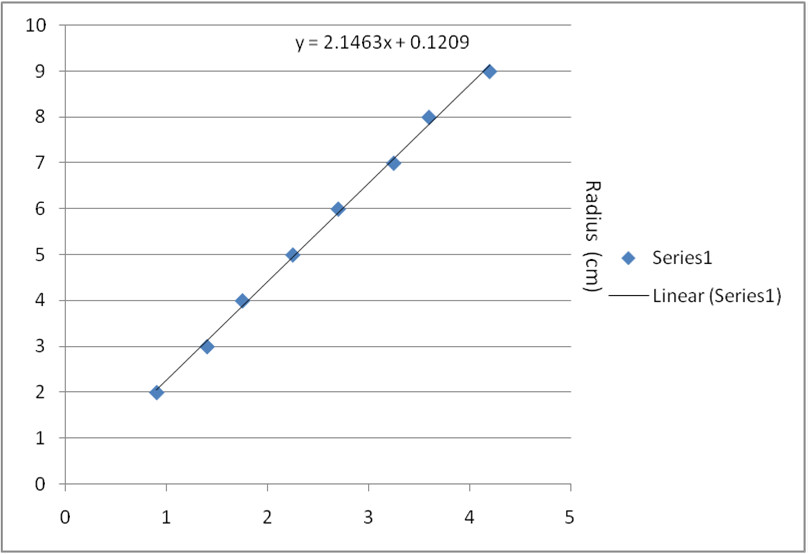
From this graph, we saw that the relationship between the height and the radius is linear and direct. The slope happened to be 2.146. When the original formula is rearranged, we can see that the proportionality constant is equal to the square root of (4/(n^2 - 1)), which also happens to be the slope of this graph. When we solved for the index of refraction, we recieved a value of 1.36.

Conclusion

Using total internal reflection, we were able to measure the index of refraction of water.The accepted value of the index of refraction of water is 1.33. Our result was pretty close to the accepted value. I also wanted to use different liquids to get a better understanding of what was going on. Hopefully, my project will give future WISE students the inspiration to experiment further.

Jahnavi Sajip February 2008

Home  Laser Teaching Center