Introduction

My project came about after Dr. Noé read my bio and, while I was wondering what optics-related project I might do, suggested I consider something related to sound and music. Both he and my father recommended a book by Thomas D. Rossing, The Science of Sound. I found myself very interested in many of the concepts it presented, as it provided a physical and mathematical background to the musical techniques I have become so familiar with over the years. Because voice and piano are my two main instruments, I became especially interested in the physics of the piano and of the human vocal tract. Both these topics relate to musical waveforms and the partial frequencies they contain. I looked for and eventually found a suitable spectrum analyzer program for my computer and used it for two separate studies, on the inharmonicity of different notes on my piano at home, and of the distinct waveforms that I could create as I sang different vowel sounds.

Partial Frequencies and Harmonics

Any complex tone can be described as a series (summation) of many simple periodic waves with unique amplitudes, phases, and frequencies, and each of these is called a partial frequency. The perceived pitch of the note being played is normally determined by the first or lowest partial, the fundamental frequency. In some instruments the partial frequencies are very close to integer multiples of the fundamental frequency, but in others they are not. This deviation from an exact harmonic relationship is called inharmonicity.

Fourier Transforms and Frequency Analysis Software

The actual propagating wave of the complex tone will be a rough and imperfect sine wave, as all of the harmonic frequencies are interfering with the wave of the fundamental, and this is what is visible on the oscilloscope.

The frequency analysis software we used does a Fourier Transform of the oscilloscope view, which in short means it mathematically breaks down something(in this case, the periodic function of a sinusoidal musical pitch) that can be described as a series, into its parts as per the general formula:

I ended up testing several free spectrum analysis packages before finding one that was satisfactory. These included iSpectrum, Audacity, WavePad, Spek, and Soundview. Eventually I found "Voice Analyzer" which was almost free ($4 from the Mac App store) and which proved to be very useful for this project. Audacity did have the ability to play any frequency I designated for any amount of time, which was useful for testing Voice Analyzer.

Voice Analyzer displays for 258 and 75 Hz tones created with Audacity

"Voice Analyzer" has both a "Spectrum" and a "Spectrogram" (plots frequency on the y axis and time on the x axis with intensity depicted by different colors) setting, but the "Spectrum" setting is a much more conventional frequency analysis interface, as it plots sound intensity (in dB) against frequency in real time, and so the data was taken using that format.

Vocal Formants

Rossing describes how spoken and sung vowel sounds are recognized by the brain based on which partials appear most prominently in their frequency spectra. These peaks in the sound envelope representing the resonances in the vocal tract are called formants. These resonances are easily observed with a frequency analyzer.

Diagram from Hyperphysics [5]

In my experiment, I chose a single pitch - A4 - and, without varying pitch or intensity, changed my vowels. I sang "Ah", "Eh", "Ee", "Oh", and "Oo", and observed both the waveforms on an oscilloscope and the frequency spectra created by the spectrum analysis software. In this case, I activated "formant normalization" mode, which is supposed to display an envelope function rather than specific, small peaks. (However, I found later that turning off formant normalization did not make a huge amount of difference, as I did not appear to have many or any inharmonic partials in my voice.)

"Ah":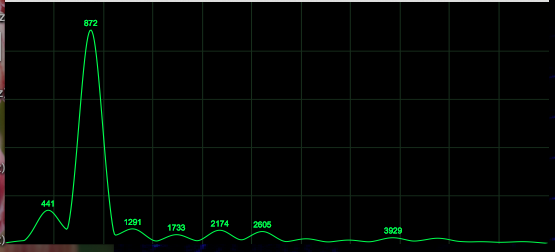

"Eh":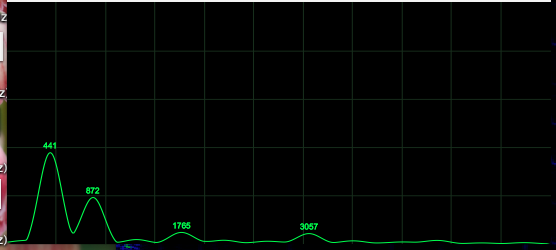

"Ee":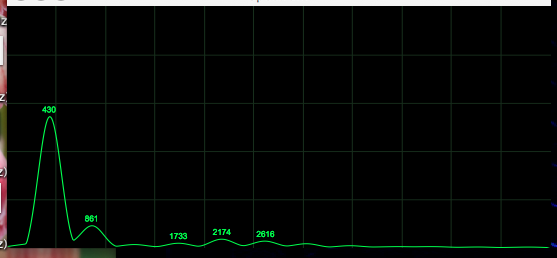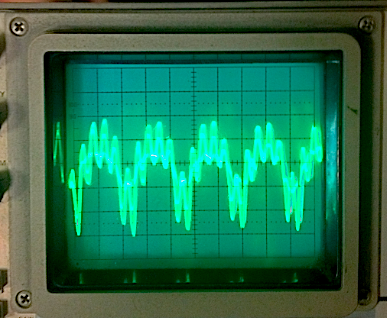

"Oh":

"Oo":

The data shows strong evidence to support Rossing's claim that vowels are recognized by their most prominent partials. Additionally, not only were my vocal formants clearly recognizable, finding them provided an interesting approach to understanding an application of Fourier Analysis.

Inharmonicity in Piano Strings

A note played on a piano will have an observable fundamental frequency as well as several harmonics. However, piano strings- particularly the large, heavy bass strings- are not ideal strings; they have some stiffness, in a sense making them party string-like and partly bar-like. The resulting restoring force in the strings resist vibration and raise the harmonics of each pitch slightly. This deviation in the upper partials from the ideal harmonic series is called inharmonicity, and it varies with the square of the partial number [Rossing, p. 290].

To study these effects, I used my piano at home (a 1972 Yamaha U1 52" upright) in an otherwise quiet environment. I chose 12 notes up the length of the keyboard: Bb1, D2, G2, A2, B2, D3, G3, C4 ("middle C"), A4, F5, B5, and D6. Keeping the sustain pedal down, I struck each note and immediately took a screen shot of the spectrum displayed by Voice Analyzer, so as to capture all possible harmonics before they died out. These 12 spectra and their subsequent analysis are summarized in a Microsoft Excel spreadsheet and the following table.

Taking into account a formula mentioned by Rossing:

where r is the radius of the string, T is the tension in the string, E is its Young's Modulus, and L is its length, it makes sense that we found much higher inharmonicities for the upper notes; those strings are much shorter, and as the L value decreases, the A value therefore increases.

Dr. Noé and I became very interested in piano tuning, especially after learning a piece of information that Dr. Noé's friend, a piano tuner by profession, gave us. Below a certain note (roughly G2), the fundamental is almost indistinguishable and these notes are therefore tuned by their upper harmonics. This phenomenon is visible in our data, but we were interested in seeing how inharmonicity plays a role. Dr. Noé and I managed to compile- for one note of our choosing, Bb1- what frequencies the fundamental and harmonics should have ideally and what the observed frequencies were, and plotted them in such a way to show this frequency ratio vs. the partial number, n.

Conclusions and Unanswered Questions

The data taken certainly reaffirmed many of the pertinent concepts mentioned in Rossing's book, in that the piano inharmonicity data showed the large discrepancy between the bass strings and the upper strings, and the vocal waveforms were hugely different among vowel sounds. However, one large outlying question that Dr. Noé and I are still unsure of pertains to the vocal formants. Often, and to no fault that I can understand, the human vocal tract is equated to a resonating tube closed at one end; however, if this is the case, only the odd harmonics should be visible (n=1,3,5,etc.), but the even harmonics- particularly the 2nd and 4th because upper partials are always harder to detect- were constantly visible while I was singing. We have yet to understand how to account for this discrepancy.

Acknowledgements

I would like to wholeheartedly thank Dr. Noé for not only giving me crucial information to complete my project, but doing so with such genuine enthusiasm and for guiding me, and allowing me to pursue subject matter that I am personally interested in. I would also like to thank Carolyn and Rachel, who have helped me with every step of the research process; I owe much of my success to them.

References

1. Rossing, Thomas D. The Science of Sound, second edition. Addison-Wesley, 1982.

2. Olsen, Harry F. Music, Physics, and Engineering Dover Publications, 1967

3. Tao, Terence. Fourier Transform. Department of Mathematics, UCLA, Los Angeles, California.

4. Beth Harris, Clear Note Piano, Boston, private communication.

5. Hyperphysics, The Acoustics of the Singing Voice.

6. Huckvale, Mark. Make Your Own Vowel Resonators! Speech, Hearing, and Phonetic Sciences, University College London, 2008.

7. Wikipedia, Harmonic.,Piano Key Frequencies

8. Piano Tuning with Verituner, http://daffy.uah.edu/piano/

9. University of New South Wales, Formant: what is a formant?.

10. Voice Analyzer by Dexus, Mac App Store

11. Young, Robert M. The Journal of the Acoustical Society of America, Volume 24 No. 3. Inharmonicity of Plain Wire Piano Strings.